HTH L-Modelle

Sie sind hier : HTH-Startseite -> Übersicht Theorieseiten -> L-Modelle

L-Modelle

Erklärungen zu den Induktivitäts-Parametern !

Jeder Lautsprecher, dessen Schwingspule auf eine bestimmte Ohmzahl gewickelt werden soll, hat als Nebeneffekt auch ein induktives Verhalten.
Im Gegensatz zu kaufbaren Drosselspulen, wo der Innenwiderstand gering ist und die gewünschte Induktivität genau und sehr konstant ist, ist es bei Lautsprechern umgekehrt : Hier überwiegt der gewünschte Innenwiderstand R, erst ab höheren Frequenzen bekommt die Induktivität L massgeblichen Anteil.
Leider ist dieses L beim Lautsprecher nicht konstant, so dass man es durch eine Ersatzschaltung von einem bedämpften und einem unbedämpften L viel besser annähern kann.

Diese elektrischen Komponenten eines Lautsprechers stellt man in Ersatzschaltbildern dar :

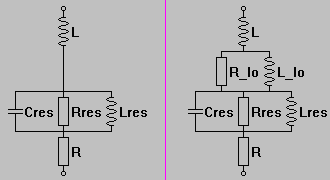
Lautsprechermodell mit einstufiger (links) oder zweistufiger (rechts) Induktivität.

Um die 3 Bauteile Cres, Rres und Lres, mit denen die Impedanzbeule bei der Resonanzfrequenz nachgebildet wird, brauchen wir uns hier nicht zu kümmern. Diese lassen sich perfekt aus den Thiele-Small-Parametern rekonstruieren !

Das einstufige L-Modell :
Dies bildet bereits das bei höheren Frequenzen zunehmend induktive Verhalten eines Lautsprechers nach. D.h., dass jeder Lautsprecher sozusagen schon eingebaut seine eigene Frequenzweiche 1. Ordnung mitbringt. Denn die Spule L bewirkt, dass bei hohen Frequenzen weniger Strom durch den Lautsprecher fliesst.
Liegen in einem Datenblatt keine ausführlicheren Angaben vor, kann das einstufige Modell durchaus gut zur Simulation verwendet werden. Bei Hochtönern reicht das in der Regel auch vollkommen aus.

Das zweistufige L-Modell :
In der Realität haben Lautsprecher bei mittleren Frequenzen deutlich höhere Induktivitätswerte als bei hohen Frequenzen, nämlich ca. 1.5- bis 3-fach. Dies bildet man schaltungstechnisch dadurch nach, dass zum L eine weitere bei tieferen Frequenzen wirksame Spule L_lo in Reihe geschaltet wird, die dann für höhere Frequenzen zunehmend durch deren parallel geschalteten Widerstand R_lo überbrückt wird.
Im Vergleich zum 1-stufigen Modell fällt hier das L etwas kleiner aus, da ja noch ein ca. 0.5- bis 2-faches bedämpftes L_lo hinzukommt.
Mit gut ermittelten Parametern des 2-stufigen Induktivitätsmodells lassen sich die typischen existierenden Lautsprecherverhältnisse sehr realistisch nachsimulieren.

In den von HTH erstellten A&D-Audio-Datenblättern sind die Parameter für beide L-Modelle angegeben. Zu verwenden ist jedoch immer nur eines, also entweder das einstufige oder das zweistufige !
Das HTH-Simulationsprogramm Weichen.Exe kann ab Version 5.4 beide L-Modelle, also das einstufige und das zweistufige, simulieren !

Wofür benötige ich diese Parameter ?

Für realistische Simulationen von Lautsprecherverhalten an Frequenzweichen, insbesondere bei Trennungen "nach oben" (Tiefpässen). Denn am oberen Ende seines nutzbaren Frequenzbereichs verhält sich der Lautsprecher zunehmend induktiv.

Für eine schnelle Eingabe in ein Simulationsprogramm. Mit nur drei Zahlenwerten wie beim 2-stufigen L-Modell lässt sich bereits ein fast perfektes Modell simulieren !
Noch besser wäre nur die Eingabe einer langen Tabelle von Impedanz und Phasenwerten für möglichst viele Frequenzwerte. Aber hierzu fehlen ablesbare Angaben in Datenblättern sowie standardisierte Dateiformate.
Dass die Eingabe von nur zwei Impedanzwerten ohne Phase wie bei AJ-Horn kein brauchbares Ergebnis liefern kann, versteht sich von selbst. Daher fragen Sie mich bitte nicht nach diesem Nonsens ! Durch zwei Impedanzpunkte kann ich unendlich viele realistische Kurven legen, die einen total unterschiedlichen Verlauf besitzen können. Umgekehrt kann ich aber aus den L-Modellen bei jeder gewünschten Frequenz genau Betrag und Phase der Impedanz berechnen !

Wofür benötige ich diese Parameter nicht ?

Für tief getrennte Subwoofer. Z.B. bei einer Trennung von 200 Hz oder darunter kann ich jegliches induktives Verhalten ignorieren. Hier reicht es nur mit dem Ohmschen Widerstand R (und natürlich den Resonanzbauteilen) zu simulieren !

Für direkt aktiv ohne passive Bauteile an Verstärker angekoppelte Lautsprecher.

Für Hochtöner sind diese Parameter allgemein weniger wichtig. Denn Hochtöner werden nicht bis zum oberen Ende ihres nutzbaren Frequenzbereichs eingesetzt bzw. dort zumindest nicht durch passive Bauteile begrenzt, mit denen Wechselwirkungen entstehen könnten.

Für Qualitätsaussagen : Egal ob in diesen Parametern hohe oder niedrige Werte stehen, mit Qualität hat das nichts zu tun. Hohe Induktivitäten schränken höchstens die Einsetzbarkeit zu hohen Frequenzen hin ein.

L-Modelle im Praxis-Beispiel :

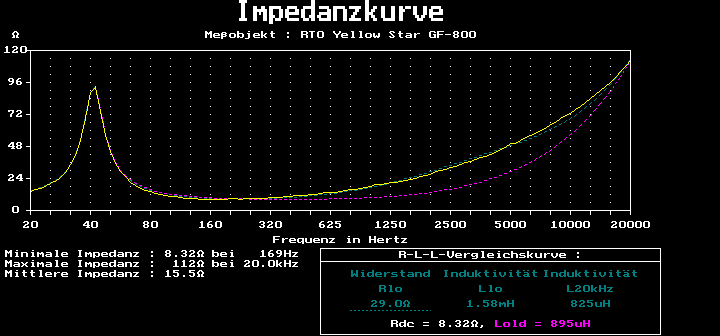
In dieser Grafik ist die real gemessene Impedanzkurve eines Chassis (gelb markiert) dem Ersatzschaltbild mit einstufigem (magenta markiert) und zweistufigem L-Modell (türkis markiert) gegenübergestellt.
Man sieht, dass beim einstufigen L-Modell eigentlich nur ein Schnittpunkt (hier bei 20 kHz) mit der realen Kurve machbar ist. Würde man den Schnittpunkt auf eine tiefere Frequenz legen, erhielte man die dort grössere Induktivität des Chassis, aber zu hohen Frequenzen hin würde die L-Modell-Kurve in magenta steil nach oben weglaufen.
Das zweistufige L-Modell kann über den gesamten Frequenzbereich die langsam nachlassende Induktivität eines Chassis sehr gut nachbilden. Lediglich kleine Resonanzspitzen wie hier bei 5 kHz lassen sich natürlich nicht simulieren.
Der 20cm-Bass aus diesem Beispiel besitzt eine aussergewöhnlich hohe Induktivität, was kennzeichnend für eine 4-Lagen-Schwingspule ist. Andernfalls ist der induktive Einfluss nicht so deutlich und die Kurven liegen dichter zusammen.

Und diese Modelle ermöglichen einen weiteren HTH-Qualitätscheck :
Neben dem Vergleich aus TSP-theoretischer Frequenzgangkurve und akustischer Frequenzgangmessung, die bei mir oft sehr gut harmoniert (Quercheck 1), habe ich durch diese L-Modell-Grafiken einen weiteren ähnlichen Check, da ich hier die TSP-theoretische Impedanzkurve direkt der gemessenen gegenüberstelle. Dies gibt mir noch mehr Sicherheit, dass meine TSP-Werte (zumindest für mein Exemplar) nahezu perfekt gemessen sind ! Denn ansonsten wäre die aus den TSP über obige Resonanzbauteile Cres + Rres + Lres berechnete Resonanzbeule im Bereich von 20 bis 80 Hz nicht so deckungsgleich = Quercheck 2 !

Formeltheorie : Und evtl. bin ich auch der Einzige, der den Einfluss der Induktivität bereits bei der TSP-Messung mitberücksichtigt ? Denn dadurch wird schon in der Theorie die Resonanzbeule, aus der die TSP ermittelt werden, leicht asymmetrisch ! Messe ich deshalb vielleicht weltweit TSP-Parameter am genauesten ?